作者：Popeller

来源：https://popeller.io/schnorr-musig2

比特币以往的多签名合约，（在使用时）都要求在交易的一个输入中使用多个签名。有了 Schnorr 签名之后，事情就不同了。得益于 Schnorr 签名的线性数据，我们可以将来自多个参与者的签名碎片组合起来，成为一个签名，然后放到交易的输入中。因此，交易的输入将只包含一个签名，而且验证者也无法分辨这到底是一个普通的单签名，还是多个签名聚合而成的签名，又或者是别的。这可以降低交易的体积并提高验证效率，（长期来看）也能提升隐私性，因为越来越多用户会开始使用 taproot。

近年来，最有前景的 Schnorr 多签名协议就是 MuSig2，由 Jonas Nick、Tim Ruffing 和 Yannick Seurin 在这篇论文中提出。所以我们就来看看这篇论文。我假定读者都熟悉 Schnorr 签名，如不熟悉，我前一篇文章有述。

多签名 vs 门限签名

MuSig2 是一个 多签名 协议，也就是 n 个参与者要集体参与（n-n）的协议。要花费一个输出的时候，n 个参与者都必须提供自己的签名。不应将它与 门限签名 协议相混淆，因为门限签名是 t-n 的，n 个潜在的签名者中只要任意 t 个签名者提供了自己的签名，即可产生有效的签名。

“多签名（multisig 或 multi-signature）” 一词在比特币世界中通常包含了门限签名和多签名两者，这可能是因为原来，这两种签名（在比特币中的实现）都使用了同一个 OP_CHECKMULTISIG[VERIFY] 脚本代码 ¹。不过，有了 Taproot，我们可以用新的方法来实现多签名（MuSig2）和门限签名（FROST），所以区别它们并使用正确的术语就变得更重要了。

MuSig2 一瞥

假设 Alice 和 Bob 想要在一个共同控制的比特币地址中接收比特币，他们可以使用 MuSig2 来生成一个地址，流程如下：

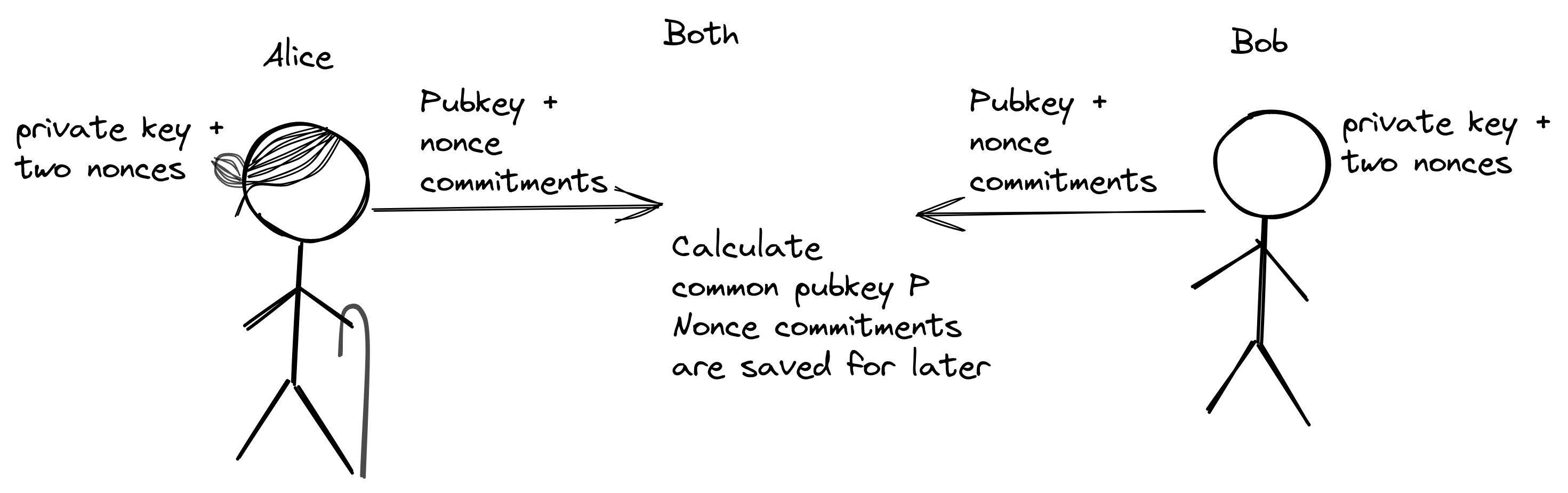
他们各自生成三个随机数：一个私钥和两个 nonce。他们各自计算出这三个随机数对应的椭圆曲线点，结果就是一个公钥和两个 nonce 承诺。他们都把这三个点分享给对方。

使用在彼此间公开的公钥数据，他们可以计算出一个共有的公钥 $P$，这个公钥就同时表示了他们俩的公钥。公钥 P 即可用来生成一个 Taproot 地址，可用来接收任何想发给 Alice 和 Bob 的资金。假设某人发送了 1 BTC 到该地址中：

现在，假设 Alice 和 Bob 想要花费这个输出，把这 1 BTC 发给地址 $Q$。Alice 或 Bob 可以创建一个未签名的交易来花费前面提到的那笔交易：

然后，他们需要集体签名这笔交易。流程大略如下：

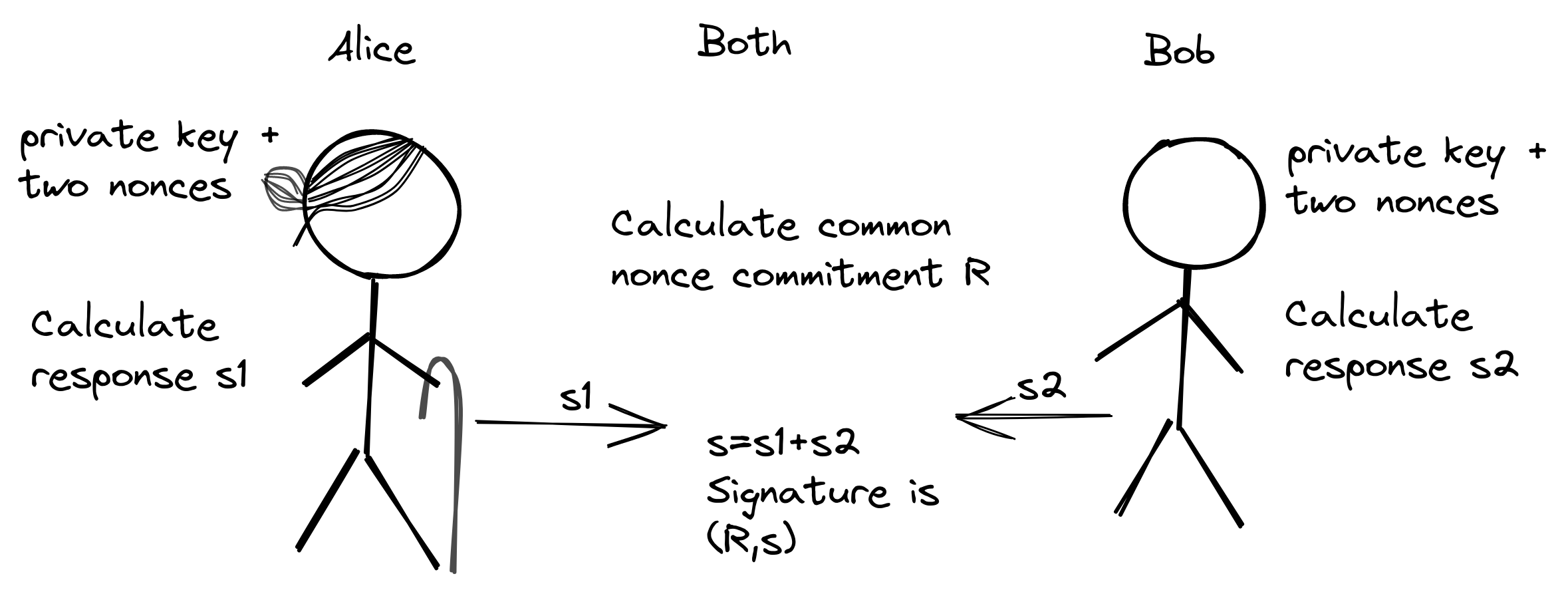
他们计算出一个共同的 nonce 承诺值 $R$ 以及各自的响应值（签名碎片） $s_1$ 和 $s_2$，最终的签名就是 $(R, s) = (R, s_1 + s_2)$。

我们来仔细看看这里的两个步骤：公钥生成和交易签名。

创建共有公钥

上一节介绍的第一步是创建一个共有的公钥，并以此生成一个 taproot 地址。

我们详细分解一下 Alice 要做什么（Bob 也做一模一样的事）：

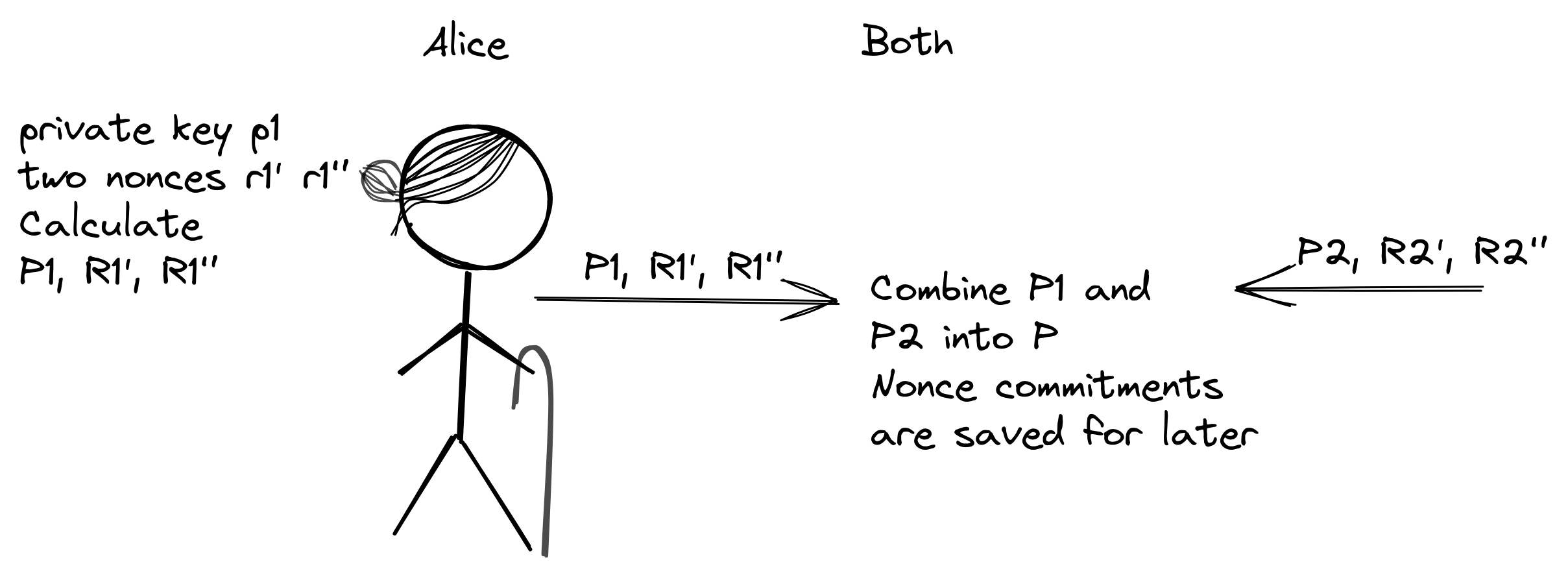
Alice 生成了自己的公钥 $P_1$ 和两个 nonce 承诺值 $R_1’$ 和 $R_1’’$，她也收到了来自 Bob 的对应的三个值 $P_2, R_2’,R_2’’$ 。然后，她就能创建共有公钥 $P$ ：

$$
\begin{align}
L &= H(P_1||P_2) \\
a_i &= H(L||P_i),\qquad i= 1, 2 \\
P &= a_1P_1 + a_2P_2
\end{align}
$$

共有公钥 $P$ 是 $P_1$ 和 $P_2$ 的线性结合。注意，两项的系数 $a_i$ 是不同的 ²，因为被哈希的数值中使用了不同的 $P_i$ 。这些系数是用来缓解 密钥取消攻击（Key Cancellation Attack）（常用名 “Rogue Key Attack”）的，这种攻击是说，Alice（先收到对方公钥的一方）可通过选择自己的公钥，使得日后无需 Bbo（对方）的参与就能创建有效的签名。我可能会写一篇文章来讲解这个题目，但现在我建议你阅读 Pieter Wuille关于这个主题的文章。

虽然 Alice 和 Bbo 交换了 nonce 承诺，这个阶段他们用不上它。nonce 承诺是日后需要签名交易的时候使用的。提前交换这些 nonce 承诺值，是为了在日后节省一轮通信。我们是在交换公钥时附带交换了 nonce 承诺。你也可以后面再交换 nonce 承诺（而且有些人认为正应该这么做 ³ ）。

Alice 使用公钥 $P$ 生成了地址 ⁴，接下来这个地址就可以交给支付者、用来接收资金了。

签名花费交易

再来看看 Alice 和 Bob 要如何合作来花费这个输出。我们照样从 Alice 的角度来理解：

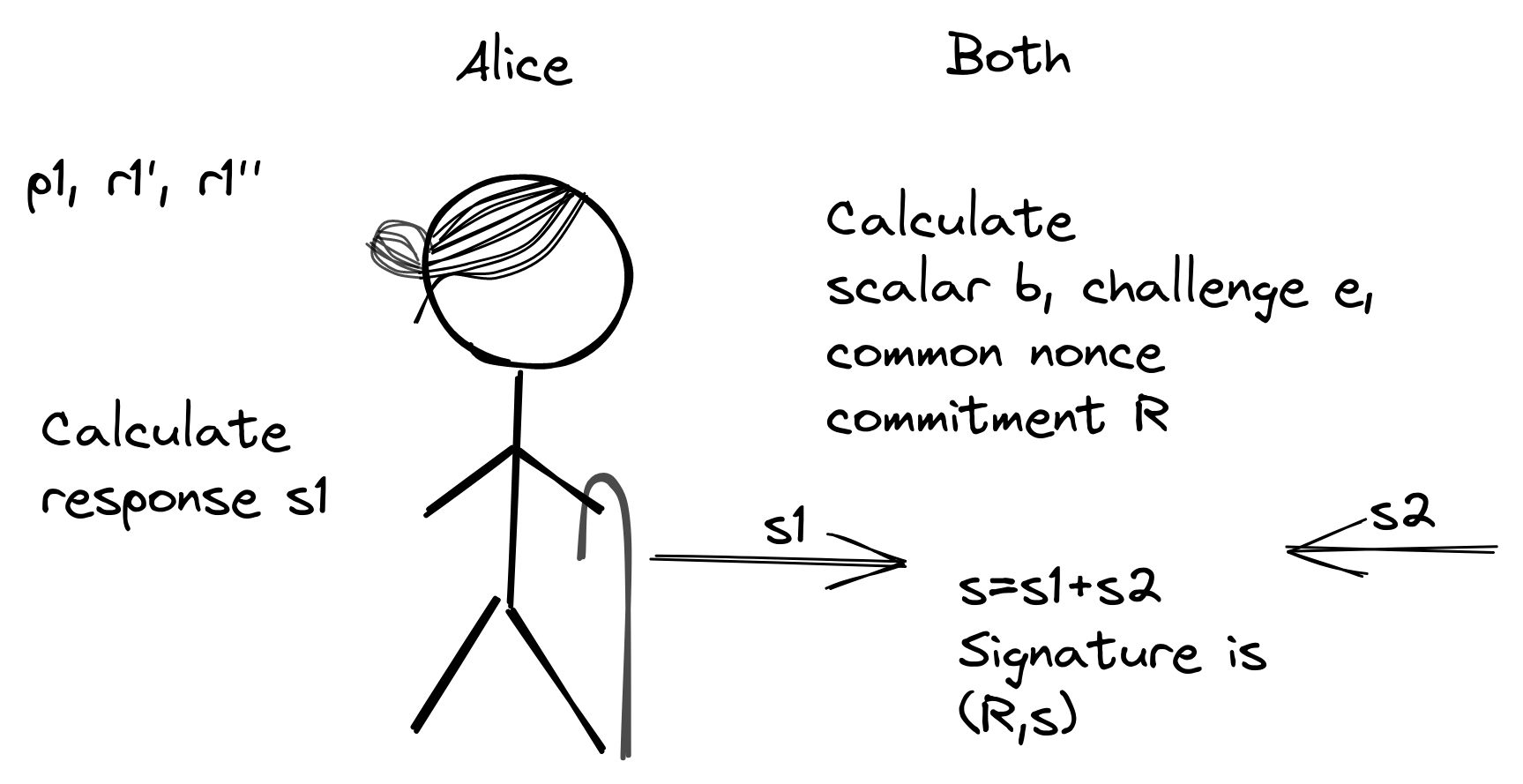
基于他们所有的 4 个承诺（以及公钥 $P$ 和待签名消息 $m$ ），他们都计算一个标量 $b$ 以及一个共用的 nonce 承诺值 $R$ ，以及一个挑战哈希值 $e$：

$$
\begin{align}
R’ &= R_1’ + R_2’ \\
R’’ &= R_1’’ + R_2’’ \\
b &= H(P||R’||R’’||m) \\
R_1 &= R_1’ + bR_1’’ \\
R_2 &= R_2’ + bR_2’’ \\
R &= R_1 + R_2 \\
e &= H(R||P||m)
\end{align}
$$

这个过程里面发生了很多事。我们的目标是让 Alice 和 Bob 能够一致使用同一个 nonce 承诺值 $R$ ，并创建他们各自的响应值 $s_1$ 和 $s_2$，最终产生一个共同的签名。为了实现这个目标，我们需要 $b$ 和 $e$ 。

他们先是用双方的 nonce 承诺值计算出标量 $b$ ，然后又使用这个标量来生成 Alice 两个 nonce 承诺值得线性和 $R_1 = R_1’ + bR_1’’$ （对 Bob 的两个 nonce 承诺值也作如此处理）。然后，这两个结果被加在一起，形成共同的 nonce 承诺值 $R$ 。这个 nonce 承诺值后面将用来生成最终的签名。

现在，轮到 Alice 来创建她的响应值 $s_1$ 了（Bob 会以类似的方式生成 $s_2$）：

$$
r_1 = r_1’ + br_1’’ \\
s_1 = r_1 + a_1ep_1
$$

注意，Alice 的最终 nonce 值 $r_1$ 是其初始 nonce 值 $r_1’$ 和$r_1’’$ 的线性和，这个线性和反映了上面 $R_1$ 的计算方式。

Alice 和 Bob 交换 $s_1$ 和 $s_2$，然后他们各自都可以生成一个有效的签名 $(R, s) = (R, s_1 + s_2)$。这个签名可以放到交易的见证数据中，然后这个交易就可以广播出去了。

这一套真的行得通吗？

Alice 和 Bob 做了许多花里胡哨的操作来生成这个签名。我们来看看这个签名是不是真的有限。Schnorr 签名的验证函数是：

$$
sG = R + eP
$$

那我们就来推导一下等式是否成立：

$$
\begin{equation}
\begin{split}
sG &= (s_1 + s_2)G \\
&= (r_1 + a_1ep_1 + r_2 + a_2ep_2)G \\
&= (r_1 + r_2 + a_1ep_1 + a_2ep_2)G \\
&= (r_1’ + br_1’’ + r_2’ + br_2’’ + a_1ep_1 + a_2ep_2)G \\
&= R_1’ + bR_1’’ + R_2’ + bR_2’’ + a_1eP_1 + a_2eP_2 \\
&= R_1 + R_2 + e(a_1P_1 + a_2P_2)\\
&= R + eP
\end{split}
\end{equation}
$$

看起来这个签名对正确的私钥集合（ $p_1$ 和 $p_2$ ）是有效的。但，我们怎么知道错误的私钥组合无论如何都只能生成出无效的签名、以及签名不可能以其它的方式伪造呢？所有这些问题都在 MuSig2 论文里面有证明，但我不能说完全理解了他们给出的证明，所以我无法验证这个方案的安全性。所以一定程度上，我得信任他们。

结论

MuSig2 比传统的、使用 OP_CHECKMULTISIG[VERIFY] 实现的多签名方案更复杂，但从验证效率、隐私性和交易的体积角度来看，这些额外的复杂性是值得的。我预计还要很长的时间才能看到它在比特币钱包中的实际实现，甚至我也不确定 MuSig2 会成为大家首选的协议。迄今为止，MuSig2 没有什么竞争者，但可能 FROST（一种用于门限签名的协议）可能会用作多签名设定。我还不知道那是不是做得到，但我会在后续的文章中探讨。

致谢

感谢这些朋友花费他们宝贵的时间对本文提出反馈：Ruben Somsen、Jonas Nick 和 Samuel Dobson。

– – –

1. OP_CHECKMULTISIG[VERIFY] 在 taproot 地址中已经不可用了（见 BIP342），但有了一个新的操作码 OP_CHECKSIGADD，可以用来实现同样的目标，并且效率更高。注意，MuSig2 和 FROST 都不使用这个新的操作码。感谢 Samuel Dobson 指出这一点。↩

2. 一个稍有改动的变种叫做 “MuSig2*”，将其中一个系数设为 1，以使公钥生成函数稍微更有效率一些。这是在一份 MuSig2 的规范草案中描述的，也在 MuSig2 论文的末尾。↩

3. (感谢 Samuel Dobson 和 Jonas Nick) 生成 nonce 并交换 nonce 承诺值的操作可以推迟到签名的时候再做，一定程度上可以降低 nonce 重用的风险，但会引入额外的一轮通信，可能会让协议变得更复杂。↩

4. 在一个合适的 taproot 地址中，公钥 $P$ 是一个 内部公钥，它会用其它花费条件的哈希值 t 来调整，因此 $P_{external} = P + tG$。用来生成地址的实际上是 $P_{external}$，但我们暂时忽略这一点，让案例更简介。我们假设 t = 0 。↩

（完）

Popeller2022-01-18
https://www.btcstudy.org/2022/01/18/schnorr-musig2-by-popeller/