作者:ochekliye enigbe
来源:https://enigbe.medium.com/randomness-signature-scripts-and-transaction-malleability-51f4ee1c2cbd
隔离见证的激活带来了一系列的变更,包括对交易不定形(transaction malleability)的修复 —— 所谓交易不定形,就是交易的标识符(整个交易的 SHA256 哈希值)会在交易内涵没有变更的情况下改变。一个交易通常包含下面几个字段:版本、交易的输入(包含前序交易的哈希值、输出的索引号、签名脚本、sequence)、交易的输出(包含面额以及公钥脚本)以及 locktime(时间锁)。
这些字段除了签名脚本之外都不能改变,不然会使交易作废。在交易被哈希之前,包含解锁脚本的字段会被清空(因为一个签名不能签名自身),因此有可能改变解锁脚本而不使交易的其余部分作废。就因为因为这一点,不同的解锁脚本可以表示同一笔交易。这是为什么呢?
一开始,我以为这跟签名的计算方式有关;用来签名交易的算法中嵌入了随机性。
从我的角度看,理解签名过程的底层数学原理应该会有所启发。因此,在本文中,我会解释我对签名的基本数学的理解、为什么不同的签名(延伸来说是解锁脚本)可以用在同一笔交易上、为什么隔离见证能够修复交易不定形问题。
签名的基本数学
签名是一种证明签名者知晓(或者说拥有)一个秘密值(即私钥,记为 e)而无需公开这个值的方法。我们知道,在非对称密码系统中:
eG(x,y)=P(x,y)eG(x,y)=P(x,y)
- 等式 1. 使用私钥和生成点计算公钥 -
这里的 G 就是生成点,P 就是 e 的公钥。
要签名一个交易哈希值时,需要选择一个随机数 k,使得:
kG(x,y)=R(r,y)kG(x,y)=R(r,y)
- 等式 2. 计算签名 -
我在这里假设了 G 在椭圆曲线上,R 也在椭圆曲线上,因此,可以用曲线上的两个点(以及加法)得出 R 的位置(加法在一个有限域中是封闭的)。这样的点 (u, v) 可以由签名者选出,如下图所示:
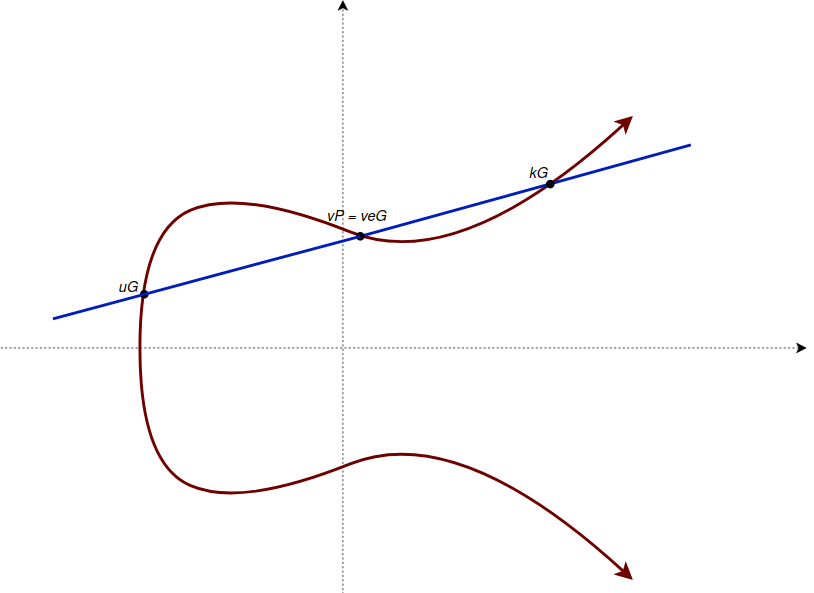
- 图 1. 椭圆曲线以及曲线上的 uG、vP 和 kG 点 -
uG(x,y)+vP(x,y)=kG(x,y)uG(x,y)+vP(x,y)=kG(x,y)
- 等式 3. 离散对数问题 -
vP(x,y)=(k−u)G(x,y)vP(x,y)=(k−u)G(x,y)
已知 eG = P,则可以转化为:
veG(x,y)=(k−u)G(x,y)e=(k−u)/vveG(x,y)=(k−u)G(x,y)e=(k−u)/v
- 等式 4. 签名的目标 -
等式 4 可以理解为离散对数问题(discrete log problem)的另一种形式,因为要么你知道 e,可以选出 k 使得 (k - u) / v = e (从而解出 eG = P),那么你就只能用暴力尝试的办法来找出成立的 (k, u, v) 数组。
在为一笔交易生成一个有效的签名 S(r, s) 之时,我们需要:
- 得出交易的哈希值 z —— 注意,需要清空解锁脚本并添加适当的签名哈希标签
- 选出一个随机数 k
- 计算 kG = R(r, y) 并取出其 x 坐标值 r
- 计算 s,使得交易的哈希值 z 与私钥 e 可以通过下面的方式选出的 u 和 v 结合成签名:
u=z/s;v=r/ss=(z+re)/ku=z/s;v=r/ss=(z+re)/k
r 和 s 就构成了对该交易的一个有效的签名。
为什么不同的签名脚本可以用在同一笔交易上
由上可知,任何能够满足上述等式的 k(不能重复使用,对每个签名都是唯一的)、u 和 v 的组合都是对给定签名哈希值 z 的有效签名。从签名者的角度看,这当然很好。因为交易的签名者可以签名同一笔交易许多次,为同一笔交易生成不同的有效签名。签名会被嵌入到交易的签名脚本中,然后广播到网络中。
但是,网络中的一些恶意用户可以在收到广播过来的交易后,稍微改变它、创建出一笔新的、变形了的有效交易;新交易在本质上与被广播的交易没有什么不同,但却具有不一样的交易 ID。这些交易花费同样的输入、给同样的输出转移相同的价值,因此会相互冲突,只有其中一笔才能挖出、加入到账本中。如果变形了的交易被挖出了,原交易会因为花费同样的输入而无法上链。
那么交易可以怎么变形呢?恶意用户可以修改签名脚本的签名格式、为签名脚本加入额外的指令、在签名脚本上使用加密技巧(见 Rosenbaum(2019) )。基本上,改变了交易的签名脚本,就会改变交易的序列化形式,从而改变交易的标识符。
隔离见证与交易不定形的修复
隔离见证提议将签名脚本数据移到另一个字段 —— witeness 字段,并且该字段不会用于计算交易 ID,所以签名脚本字段的变化不会影响交易的标识符。
结论
随机性以及每个签名唯一的 k 的选取,让签名者可以让交易数据产生变化。他们可以为一笔交易生成不同的签名,虽然最后只有一个会嵌进解锁脚本中。在隔离见证实施以前,签名后的交易在广播过程中,用户可能会遭遇变形攻击:恶意用户可以修改广播交易的签名脚本字段,从而改变交易的标识符。而有了隔离见证,签名脚本的数据会移到一个不影响交易 ID 计算的字段中,从而消除了变形攻击界面。
注:
如有任何反馈,不胜感激。不论是觉得本文有用,还是发现了事实性错误,请不吝在在我的推特 @engb_os 中留下评论。
参考文献:
- Antonopoulos, A. (2017). Mastering bitcoin: Programming the open blockchain
- Song, J. (2019). Programming bitcoin: Learn how to program bitcoin from scratch
- Rosenbaum, K. (2019). Grokking Bitcoin
(完)
ochekliye enigbe2022-04-25
https://www.btcstudy.org/2022/04/25/randomness-signature-scripts-and-transaction-malleability/