作者:Cashu Developer

- Cashu 坚果全家桶 -
Chaumian ecash 的一个标志性的特征是其钱币的取款(发行)与存款(赎回)是无法关联起来的(unlinkability)。不同的 ecash 实现运用了多样的密码学方法来实现这种效果,其中最突出的 “盲签名(blind signatures)”。盲签名是 Chaum 发表于 1982 的著名论文中的真正发明。就像许多标准的密码学方法一样,盲签名是一种密码学 “原语” —— 一种砖块 —— 可以用来构筑更大、更复杂的密码学系统。
本文会介绍 Cashu 中的盲签名的基本原理,并解释为什么 ecash 通常只能使用少数几种钱币面额,比如 2 的幂(1、2、4、8、16、32 聪,等等),来表示价值。我们先要了解盲签名是怎么工作的、实现了什么效果。我们会先从一个更加正式的定义开始,然后提出一个简化的例子,展示如何以盲签名为核心、构造一种支付系统。
给定一条消息,用户 Alice 可以盲化这条消息(称作 M',这个记号表示盲化),从而没有人能发现新消息和原消息之间的关联。Alice 把这条盲化后的消息展示给铸币厂 Bob,而 Bob 会给出一条对它的密码学签名 C'。只有 Alice 才能还原这个盲签名,使之成为一个(没有盲化的)签名 C。神奇的地方在于,C 正好是对原消息 M 的签名,虽然 Bob 从未见过 M。你可能已经猜到了,(M, C) 这样的元组就是我们的 ecash 钱币。
人们也常常使用著名的 “碳纸信封” 来演示盲签名。先想象一份打印在之上的合同 M。Alice 希望 Bob 给这份合同签名,但又不希望 Bob 知道其中的内容。为此,Alice 先把合同 M 塞进一个由碳纸制成的信封里面。然后,我们把这个封好的信件 M' 交给 Bob。Bob 可以 不打开信封,直接在信封上签名 ,然后把签好名的信件 C' 交给 Alice。当我们取出合同的时候,我们可以看到 Bob 的签名 C 已经在原合同 M 上了,虽然 Bob 从未见过这份合同。
这里还有一张图,展示了 Cashu 的盲签名方案所用的盲化、签名、还原、以及验证步骤。最重要的是,Alice 的钱包对 (M, C) 的操作是在 “光明世界” 了的,而铸币厂是 Bob 只能看到 “失明世界” 里的 (M', C') .
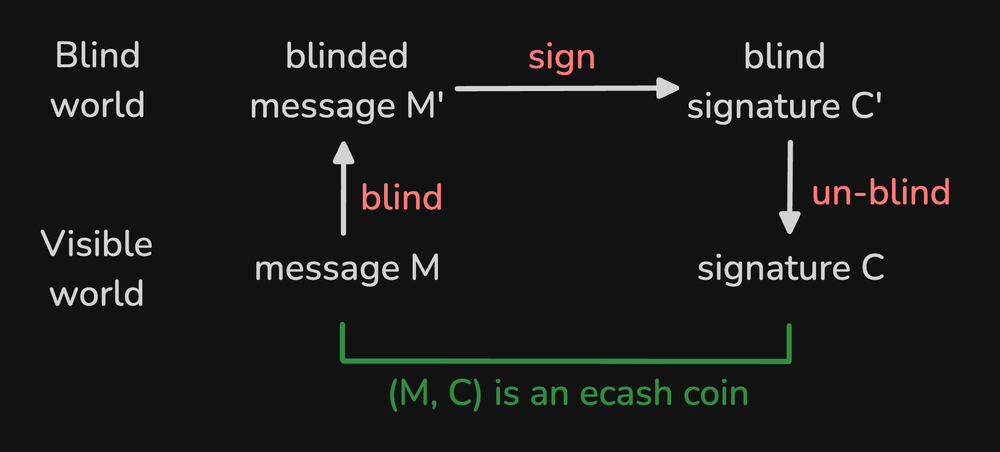
带有价值的盲签名
现在,我们已经对盲签名方案的工作原理有了基本的了解,来看看铸币厂如何为发放给用户的签名赋予价值。
为了给自己的签名赋予价值,Bob 决定仅在 Alice 给他支付一定数额 a 的底层货币(比如,a 是 128 聪 的比特币)时,才会提供签名 C' 。Bob 也承诺会给任何能够在日后出示元组 (M, C, a)(分别代表原消息、签名和数额)的人 —— 不论是 Alice 还是她的收到了 ecash 的朋友 Carol —— 退还资金。这意味着,我们可以将元组 (M, C, a) 当成一枚钱币,是可以在用户间转移的钱币(比如,Alice 可以把它发给 Carol)。
那么 Bob 如何验证一枚钱币 (M, C, a) 真的价值 a(即,128 聪),既不是更贵、也不是更贱呢?为了理解这一点,我们需要在我们的盲签名方案中引入另一个细节,就是 Bob 要使用自己的私钥 k 来创建签名。实际上,这是一种简单(但不可逆转)的乘法,用私钥 k 乘以 Alice 所提供的盲化消息:C' = k * M'。
为了将一个具体的数额 a 绑定到这个签名上,Bob 还要为每一种可能赋予钱币的数值都生成一个私钥,也就是说,Bob 有很多个私钥 k_a,而这里的索引号 a 就表明了该私钥所代表的数额。当 Bob 以后要为钱币验证签名时,他将使用跟数额相对应的私钥 k_a。这样一来,他就能确定,钱币 (M, C, a) 中的数额 a 没有被篡改。在 Cashu 中,我们把对应于所有可能数额的所有签名密钥称做 “密钥集(keyset)”。
侧边注:聪明的读者会意识到,严格来说,C' 并不是一种签名,而更像是一种消息认证码(MAC),因为它不能使用我们已经介绍的工具来公开验证。不过,对于我们当前的目标来说,这并不重要,所以我们暂时忽略这个细节。
数字中的隐私
现在,我们已经打好了基础、介绍了这套签名方案的所有相关元素,可以转向这篇最重要的部分了:为什么 ecash 系统常常限制他们所支持的钱币面额(比如限制在使用 2 的幂上)?如前所述,铸币厂 Bob 需要为每一种面额使用一个特殊的私钥,以保证钱币的面额没有遭到篡改。然而,如果没有正确处理,这就会带来一个严重的问题:如果钱包可以使用任何整数作为自己的有效面额,那么铸币厂跟踪单个单个的钱币的生命历程(从发行到赎回)就非常容易,从而在实际上取消掉我们一开始用盲签名实现的所有效果。我们来举一个例子。
假设一个铸币厂为小到 a = 1、大到 a = N 之间的所有整数都准备一个私钥 k_a,也就是说,这个铸币厂需要 N 个不同的私钥。假设 Alice 希望铸造一个面额恰好是 1337 聪的钱币。铸币厂将使用私钥 k_1337 来创建一个盲签名,并在日后该钱币被花费的时候验证签名。
这种方法的问题在于,这种面额为 1337 的钱币的 匿名集 最大只能跟这个铸币厂已经发行过的 1337 面额的钱币的数量一样大。很容易看出,允许的面额越多,也即 匿名桶 越多,每一个匿名集就越小,这对用户的隐私性不利。
可以看出,要增加每一个匿名集的大小,一种简单的办法就是限制可以使用的面额 a 的可能性。 我们可以先将 a 限制在 2 的幂中,即 a = 2^n,然后用这些子数额组合出我们需要的任意数额。假设 Alice 想要铸造 1337 聪的 ecash 。 为此,她可以将总数额打散成一系列的子数额:1 + 16 + 128 + 256 + 1024 = 1337 。当我们支持的是 2 的幂时,找到这样的分解是很容易的。
事实上,这样的分解甚至是唯一的。我们可以通过将数的十进制表示 1337 转化成二进制表示 10100111001 来找出这样的分解。只需统计这个二进制数中哪些位置(记为 n )的值是 1 还是 0,就可以知道我们需要几个钱币:从最小位(最右边)开始,一位一位往左边数,直到最左边;如果位置 n 的数值是 1,就把数字 2 ^ n 加入我们的和中。也就是说,1337 = 2^0 + 2^4 + 2^7 + 2^8 + 2^10(5 个面额不同的钱币)。是不是很简单!
限制可能面额的后果是,现在,不论 Alice(或她的朋友 Carol )什么时候想赎回余额的一部分,她给 Bob 出示的钱币都跟 Bob 在过去发行过的许多钱币具有相同的面额。注意,如果 Alice 取出了刚好是总计 1337 聪,又立即把这么多钱存入,那这一点就不成立了。Bob 将很容易断定,这一取一存的是同一笔钱。也就是说,事实上,我们要通过(1)切分取款、部分存入;以及(2)存入之前稍等片刻,让其他曾经取款的用户可能在同一时间存入其他钱币;来获得安全性。
我们还可以看到,可能面额的集合也会影响匿名集的大小。假设在一种极端情形中,Bob 只发行面额为 1 的钱币。那么,Alice 将需要铸造 1337 个面额为 1 的钱币,才能获得自己想要的数额。然而,这样做虽然能获得最大程度的隐私性,却要面对最低的效,因为用户和铸币厂都不得不存储大量数据、在支付时传输大量数据。因此,必须选择一个合理的折中,例如使用 2 的幂分解。有趣的是,一篇发表于 1997 年的论文发现,在法定货币的价格世界里,以 2.60 为基数将产生最高效的分解(数额表示)。
一键隐藏
就像许多其它情形一样,密钥集大小的选择也可以归结为效率和隐私性的取舍。更大的密钥集允许你更高效地表示数额,但也让钱币更容易被跟踪,反之亦然。不过,还有另一种解决方法,是我们这篇文章没有触及的,就是 “数额盲化”。使用跟 “机密交易(confidential transactions)” 类似的技术,我们可以用零知识证据来隐藏交易中的数额,就像在 Liquid 侧链、门罗 密码货币,以及 WabiSabi CoinJoin 协议中那样,我们可以将铸币厂的跟面额对应的私钥换成唯一一把私钥,并用它来创建所有签名。这将允许钱币使用任意的面额,同时提高整个系统的隐私性,因为将只有一个匿名集(因此其规模也是最大的)。
在这个例子中我们可以看出,匿名性和效率的取舍并不是自然规律,而大大取决于所用的密码学方法。在我们冒险进入 Chaumian Ecash 研究和 Cashu 系统开发的新领域时,请对这个方向上的更令人激动的进展保持关注。
在那之前,永远要记得:Pricey loves company(译者注:可能的意思是,要隐藏在众多同类中,才能具有隐私性,可译为“藏叶于林”)!
(完)
Cashu Developer2024-12-13
https://www.btcstudy.org/2024/12/13/buckets-of-blind-signatures/